독립시행의 확률
확률은 일상생활에서 우리가 예측할 수 없는 사건들의 발생 가능성을 수치화한 개념입니다. 특히 독립시행이란 특정 사건이 일어나는 확률이 다른 사건의 결과에 영향을 받지 않는 경우를 말합니다. 이 글에서는 독립시행의 확률에 대해 쉽게 이해할 수 있도록 설명해 드리겠습니다.
독립시행이란?
독립시행(Independent Events)은 두 사건이 서로 영향을 주지 않는 경우를 말합니다. 즉, 한 사건의 발생 여부가 다른 사건의 발생 확률에 아무런 영향을 미치지 않습니다. 예를 들어, 동전을 던져 앞면이 나오는 사건과 주사위를 던져 3이 나오는 사건은 독립적인 사건입니다.
예시 1: 동전 던지기
동전을 던지는 경우를 생각해봅시다. 동전을 한 번 던져 앞면이 나올 확률은 1/2입니다. 이 동전을 다시 던져 앞면이 나올 확률도 여전히 1/2입니다. 이 두 사건은 독립적이므로, 두 번 모두 앞면이 나올 확률은 다음과 같이 계산할 수 있습니다.

[ P(앞면 , 그리고 , 앞면) = P(앞면) \times P(앞면) = \frac{1}{2} \times \frac{1}{2} = \frac{1}{4} ]
예시 2: 주사위 던지기
주사위를 던져 특정 숫자가 나올 확률도 동일하게 계산할 수 있습니다. 주사위를 한 번 던져 3이 나올 확률은 1/6입니다. 두 번 던져 모두 3이 나올 확률은 다음과 같습니다.

[ P(3 , 그리고 , 3) = P(3) \times P(3) = \frac{1}{6} \times \frac{1}{6} = \frac{1}{36} ]
독립시행의 확률 공식
독립시행의 확률을 일반화하면, 두 독립적인 사건 A와 B가 있을 때 두 사건이 모두 발생할 확률은 다음과 같습니다.
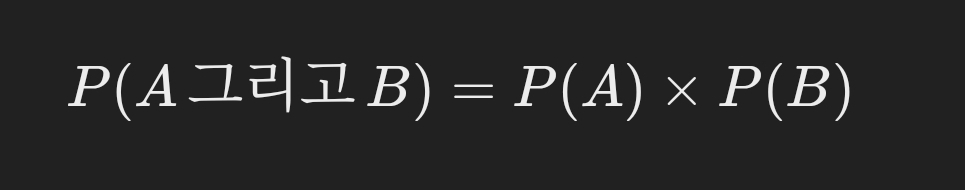
[ P(A , 그리고 , B) = P(A) \times P(B) ]
이 공식을 통해 여러 독립적인 사건들이 동시에 발생할 확률을 계산할 수 있습니다.
실생활에서의 독립시행 예시
복권 당첨
복권을 두 번 사는 경우를 생각해봅시다. 첫 번째 복권에 당첨될 확률과 두 번째 복권에 당첨될 확률은 서로 독립적입니다. 따라서 두 번 모두 당첨될 확률은 첫 번째 복권 당첨 확률과 두 번째 복권 당첨 확률의 곱으로 계산할 수 있습니다.
온라인 쇼핑
온라인 쇼핑에서 물건을 두 개 구매할 때, 첫 번째 물건이 불량일 확률과 두 번째 물건이 불량일 확률은 독립적입니다. 따라서 두 물건이 모두 불량일 확률도 독립시행의 확률을 이용해 계산할 수 있습니다.
참고할 수 있는 사이트
독립시행의 개념은 단순하면서도 중요한 확률 이론의 기본입니다. 이를 이해하면 일상생활에서 다양한 확률 문제를 보다 쉽게 접근할 수 있을 것입니다. 확률을 이해하는 것은 곧 미래를 예측하는 힘을 가지는 것과도 같습니다.